Descriptive Statistics
Correlation Coefficient
Key Questions:
- What does the correlation coefficient show?
- How do we interpret the sign and magnitude of the correlation coefficient?
- Why does high correlation not imply causation?
Warm-up: Height and Shoe Size
Each student needs to provide two personal measurements:
- Height (in centimeters)
- Shoe size
Record the data for all students in two columns and create a scatter plot (X-axis — height, Y-axis — shoe size) in Desmos.
Add a linear regression to your diagram and write down the correlation coefficient.
Theoretical Foundations
The correlation coefficient (r) measures the strength and direction of a linear relationship between two variables:
- r = 1 — perfect positive linear relationship;
- r = -1 — perfect negative linear relationship;
- r = 0 — no linear relationship (zero correlation).
Interpretation of the correlation coefficient:
- |r| < 0.3 — weak relationship
- 0.3 ≤ |r| < 0.7 — moderate relationship
- |r| ≥ 0.7 — strong relationship
Important: high correlation does not imply causation — there may be hidden factors or mere coincidences.
Continue Team Work
Each team uses their data from the previous lesson (two variables over 30 days). The task is to calculate the correlation coefficient and interpret it.
Exit Ticket
Come up with a pair of variables that you think should have a high correlation. Explain why you expect that relationship.
Scatter Plots
Key Questions:
- How does a scatter plot help analyze relationships between variables?
- What is correlation and how is it interpreted?
- How can we distinguish positive, negative, and zero correlation?
Warm-up: Collecting Data
Say the day of the week you were born and the last digit of your phone number. Record all values in two columns:
- First variable — day of the week of birth (Mon=1, ...)
- Second variable — last digit of the phone number
Build a scatter plot (X-axis — day of the week, Y-axis — last digit). Discuss whether there is any relationship between the variables.
Key Concepts
- Scatter plot – a graph showing pairs of numerical values for two variables.
- Correlation – a measure of the strength and direction of a relationship between two variables.
- Positive correlation – when an increase in one variable is accompanied by an increase in the other.
- Negative correlation – when an increase in one variable is accompanied by a decrease in the other.
- Zero correlation – there is no linear relationship between the variables.
Types of relationships on a scatter plot:
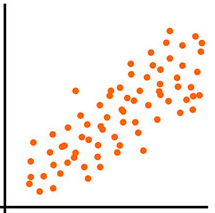
Direct (positive) relationship: points show an upward trend — increases in one variable accompany increases in the other.
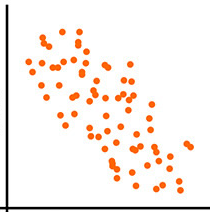
Inverse (negative) relationship: points show a downward trend — increases in one variable accompany decreases in the other.
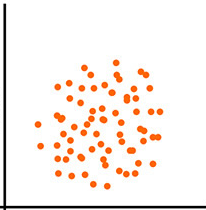
No relationship: points are randomly scattered — changes in one variable do not affect the other.
Examples: positive — ice cream sales and air temperature; negative — product price and quantity sold; zero — shoe size and math test scores.
Team Assignment
Each team must find real historical data for two variables for one month (30 observations) and record the data in any convenient format.
Task distribution:
- Teams 1–2: euro exchange rate and dollar exchange rate in KZT
- Teams 3–4: average daily temperature in Almaty and dollar exchange rate in KZT
- Teams 5–6: dollar exchange rate and ruble exchange rate in KZT
After collecting the data, build a scatter plot and analyze it:
- Describe the type of correlation (positive, negative, or none)
- Make a conclusion about the possible relationship between the variables
Exit Ticket
Think of and write down two variables for which you expect a positive, negative, and zero correlation. Justify your choice.
What is the class height?
Key questions:
- What does the mean show and how to interpret it?
- Why is standard deviation important when describing data?
- How does the median differ from the mean?
Warm-up: Arithmetic and Geometric Mean
Find the arithmetic mean and geometric mean for the following sets of numbers:
- 4, 9
- 2, 8
- 3, 6, 12
Compare: which is larger? What does this indicate?
Data Collection
Each student states their height in centimeters, and the class records all values. This forms a sample.
Additional task:
Add one realistic height so that the new mean is a whole number.
Mean and Standard Deviation
The mean is calculated using the formula:
\[\bar{x} = \frac{x_1 + x_2 + \dots + x_n}{n}\]
Standard deviation shows how much the values deviate from the mean:
\[\sigma_x = \sqrt{\frac{(x_1 - \bar{x})^2 + (x_2 - \bar{x})^2 + \dots + (x_n - \bar{x})^2}{n}}\]
Calculate these measures for your sample and draw conclusions.
Median and Comparison with the Mean
The median is the value that divides the ordered dataset in half.
Find the median for your sample and compare it with the mean.
Question: Why can the median differ from the mean?
Exit Ticket
Create a sample of 5 numbers where the median differs significantly from the mean. Explain why this happened.
Weather Data Analysis
Key questions:
- How do statistical measures help describe temperature changes?
- What does a box plot show?
- How can the median, quartiles, and standard deviation be used to analyze weather data?
Warm-Up
Each student says their height. Write all heights in one dataset.
Task: Construct a box plot based on the collected data.
Introduction: Weather Observations
Each team is assigned one month and one major city in Kazakhstan:
- Team 1 – January, Almaty
- Team 2 – March, Astana
- Team 3 – May, Shymkent
- Team 4 – July, Karaganda
- Team 5 – September, Aktobe
- Team 6 – November, Ust-Kamenogorsk
Each team should record temperature observations for two weeks of the assigned month.
Data Analysis
Steps:
- Create an ordered dataset – arrange temperatures in ascending order.
- Determine the median and quartile values (Q1 and Q3).
- Build a box plot using the calculated values.
Presentation of Results
After completing the analysis, each team selects a representative to present the results. Their speech begins with:
“We conducted a statistical analysis of weather data in [city] for [month] and arrived at the following conclusions: …”
The representative explains how the temperatures were distributed and what the plot shows.
Descriptive Statistics
Key Questions:
- What is a sample?
- How do we describe data using median and quartiles?
- How do we interpret a box plot?
Key Terms
Take turns saying your birth month number and write all numbers in one row.
Definitions:
- Sample – a set of observed values, notation: m₁, m₂, …, mₖ
- Sample size – number of observations
- Ordered dataset – same sample arranged in ascending order
Elements of a Box Plot
- Median – value that divides the ordered dataset into two equal halves.
- Quartiles (\(Q_1\) and \(Q_3\)) – values that divide data into four equal parts.
Task:
Find the median, lower and upper quartiles for birth months.
Constructing and Interpreting the Box Plot
- Construct a box plot based on the calculated values and interpret the median and quartiles.
- Which birth month appears most frequently and which values are atypical?
- Can conclusions drawn from the sample be generalized to the entire city? Why?
Practice: Constructing a Box Plot from Data
Data (15 values):
4, 7, 5, 6, 9, 7, 8, 6, 10, 7, 5, 8, 6, 9, 7
Task:
- Order the data in ascending order (create an ordered dataset)
- Find the sample median
- Find the first and third quartiles (Q1 and Q3)
- Determine the minimum and maximum values
- Draw the box plot
Exit Ticket
What would this plot of birth months look like if the sample included all residents of Almaty?